《天才与算法:人脑与AI的数学思维》读书笔记
作者:[英]马库斯·杜·索托伊(Marcus du Sautoy)
译者:王晓燕,陈浩,程国建
出版社:机械工业出版社
出版时间:2020-02
提出猜想很难,证明猜想更难!
某位教授对数学中的一个模式做了一个猜想,他的一个研究生花了十年的时间才证明了它是错误的。(博士是多么地难毕业呀!研究十年结果发现是个错的,多么地悲催。)
1、高斯猜想
素数分布函数和对数积分函数的猜想,即:Li(x)-π(x)总是正的而且是递增的。
Li(x) : 对数积分函数
π(x) : 小于x的素数个数
在高斯时代,已经证明了素数函数π(x)趋近于对数积分函数Li(x),既素数定理,而且发现Li(x)总是大于π(x),而且两个差距越来越大,这当然不会影响素数定理,因为他们之间的差的增长远没有函数值的增长快。
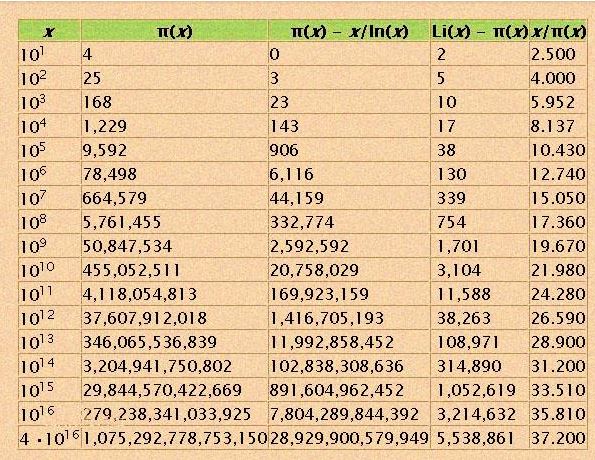
于是,高斯猜想:Li(x)-π(x)总是正的而且是递增的.
2、李特尔伍德的证明
1914年英国数学家李特尔伍德从理论上证明了事实正好相反(即存在Li(x)小于π(x))。高斯的猜想是错误的!
李特尔伍德证明了:
Li(x)-π(x)从正到负,再从负变为正,如此反复无数次。
但是我们利用目前最强大的计算机,计算到的x都是Li(x)>π(x),那么在哪里才会第一次出现Li(x)小于π(x)呢,既第一个李特尔伍德反例?
我们计算能力有限,但数学家有捷径可走,虽然他们无法准确找到第一个李特尔伍德反例值,但他们可以找到这么一个值N,然后证明第一个李特尔伍德反例值小于N,后续在逐步缩小N的取值。
直到1933年,李特尔伍德的学生斯克维斯(Samuel Skewes)首次证明,如果黎曼猜想成立的话,第一个李特尔伍德反例值一定小于这么一个数,我们称为斯克维斯数:

(参考自http://www.360doc.com/content/17/1022/21/44612658_697252201.shtml
)
这个数字太大了,表示成简单的科学计数法是:,而我们整个可观测宇宙的原子数不过是
3、哲思
究竟是什么驱使人类去证明?人类创造数学的动机是什么?编写算法来给数学家制造更多的挑战,这会成为我们探索数学领域的新动力吗?
数学的起源可以追溯到人类试图理解自己所生活的环境,预测接下来会发生什么,从而使我们更加适应环境,并选择对我们有利的事物。可以说,数学是人类的一种生存行为(我在故我思)。




发表评论: