高中奥数梅涅劳斯定理

作者：大熊空间发布时间：2022-02-19 17:09分类：无浏览：226评论：0

导读：梅涅劳斯定理设分别是三边或其延长线的点,若三点共线,则. 图片.png梅涅劳斯定理的逆定理设分别是三边或其延长线的点,若则三点共线. 将两个定理合写为: 设分别是三边所在直线(...

梅涅劳斯定理

设 $A^\prime,B^\prime,C^\prime$ 分别是 $\Delta ABC$ 三边 $BC,CA,AB$ 或其延长线的点,若 $A^\prime,B^\prime,C^\prime$ 三点共线,则 $\dfrac{BA^\prime}{A^\prime C}\cdot \dfrac{CB^\prime}{B^\prime A}\cdot\dfrac{AC^\prime}{C^\prime B}=1$ .

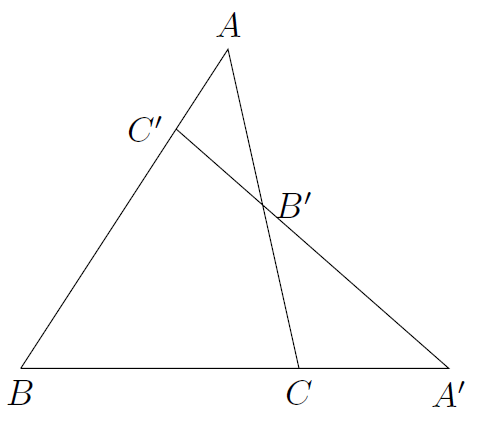
图片.png

梅涅劳斯定理的逆定理

设 $A^\prime,B^\prime,C^\prime$ 分别是 $\Delta ABC$ 三边 $BC,CA,AB$ 或其延长线的点,若 $\dfrac{BA^\prime}{A^\prime C}\cdot \dfrac{CB^\prime}{B^\prime A}\cdot\dfrac{AC^\prime}{C^\prime B}=1$ 则 $A^\prime,B^\prime,C^\prime$ 三点共线.

将两个定理合写为:
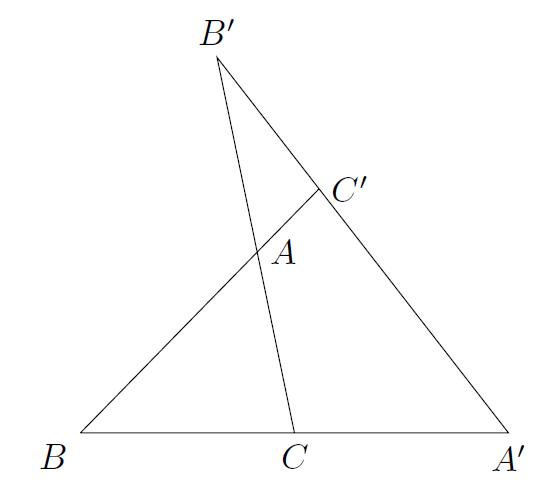
设 $A^\prime,B^\prime,C^\prime$ 分别是 $\Delta ABC$ 三边 $BC,CA,AB$ 所在直线(包括三边的延长线)上的点,则 $A^\prime,B^\prime,C^\prime$ 三点共线充要条件是 $\dfrac{BA^\prime}{A^\prime C}\cdot \dfrac{CB^\prime}{B^\prime A}\cdot\dfrac{AC^\prime}{C^\prime B}=1$

图片.png

如图，对于 $\Delta C^\prime BA^\prime,\Delta B^\prime CA^\prime,\Delta AC^\prime B^\prime$ 有下述形式的充要条件: $\dfrac{C^\prime A}{AB}\cdot \dfrac{BC}{CA^\prime}\cdot\dfrac{A^\prime B^\prime}{B^\prime C^\prime}=1;\dfrac{B^\prime A}{AC}\cdot \dfrac{CB}{BA^\prime}\cdot\dfrac{A^\prime C^\prime}{C^\prime B^\prime}=1;\dfrac{AB}{BC^\prime }\cdot \dfrac{C^\prime A^\prime }{A^\prime B^\prime }\cdot\dfrac{B^\prime C}{CA}=1$

第一角元形式的梅涅劳斯定理

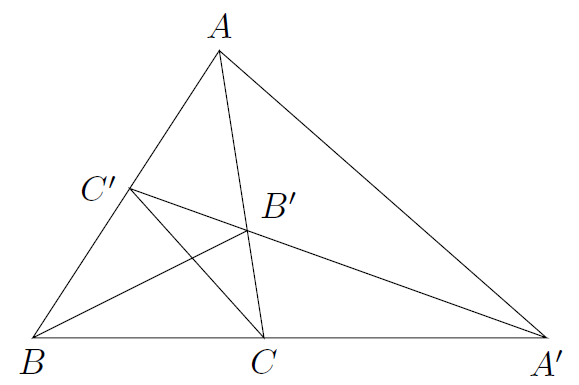
设 $A^\prime,B^\prime,C^\prime$ 分别是 $\Delta ABC$ 三边 $BC,CA,AB$ 所在直线(包括三边的延长线)上的点,则 $A^\prime,B^\prime,C^\prime$ 三点共线充要条件是 $\dfrac{\sin{\angle BAA^\prime}}{\sin{\angle A^\prime AC}}\cdot \dfrac{\sin {\angle ACC^\prime}}{\sin{\angle C^\prime CB}}\cdot\dfrac{\sin{\angle CBB^\prime}}{\sin{\angle B^\prime BA}}=1$

图片.png

第二角元形式的梅涅劳斯定理

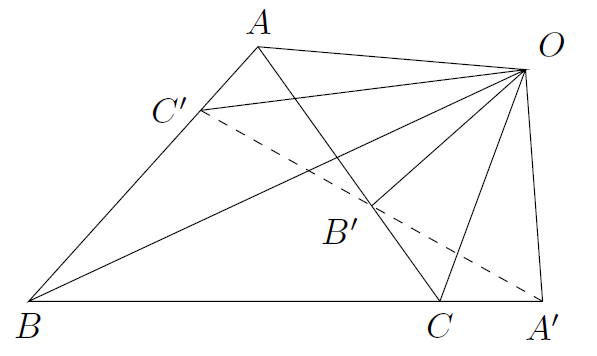
设 $A^\prime,B^\prime,C^\prime$ 分别是 $\Delta ABC$ 三边 $BC,CA,AB$ 所在直线上的点,点 $O$ 不在 $\Delta ABC$ 三边所在直线上, 则 $A^\prime,B^\prime,C^\prime$ 三点共线充要条件是 $\dfrac{\sin{\angle BOA^\prime}}{\sin{\angle A^\prime OC}}\cdot \dfrac{\sin {\angle AOC^\prime}}{\sin{\angle C^\prime OB}}\cdot\dfrac{\sin{\angle COB^\prime}}{\sin{\angle B^\prime OA}}=1$

图片.png

上一篇：Python Selenium 将网页另存下载(包含资源文件(js,css,图片等))
下一篇：推荐7个国外图片资源网站

高中奥数梅涅劳斯定理

相关文章

发表评论: 取消回复

个人资料

日历

搜索

最新评论

分类

标签

热门文章

链接

高中奥数 梅涅劳斯定理

相关文章

发表评论: 取消回复

个人资料

日历

搜索

最新评论

分类

标签

热门文章

链接

高中奥数梅涅劳斯定理